INTRODUCTION

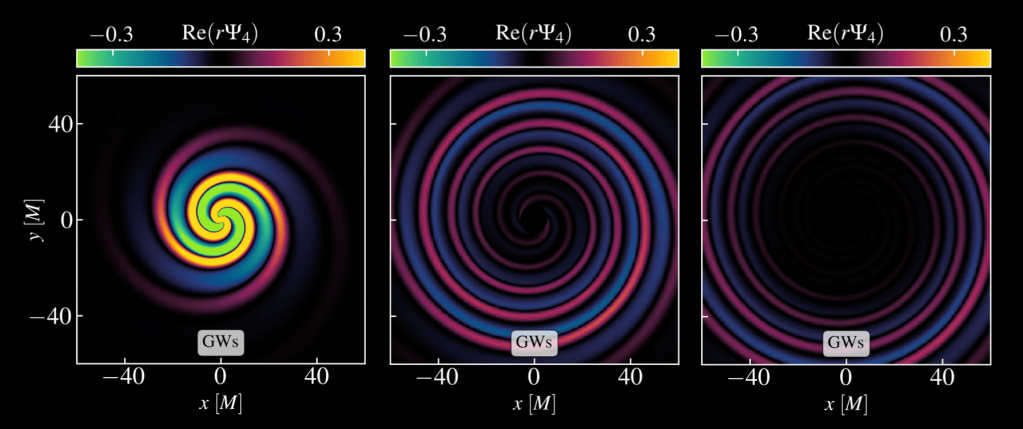
Strong Spacetime studies how black holes behave when gravity’s nonlinearity is essential, with an emphasis on stability and observable dynamics. Building on recent linear and fully non‑linear advances, we aim to extend rigorous stability results from non‑rotating (and very slowly rotating) cases to all sub‑extremal Kerr black holes—i.e., rotating holes with spin below the maximal (“extremal”) limit. These results characterize the gravitational radiation emitted by a perturbed black hole (including non‑linear memory), the way its event horizon evolves and settles, and how its final mass and spin change. In parallel, we will probe whether extremal black holes can form in realistic collapse by treating near‑extremal formation as a critical phenomenon: assessing near‑horizon linear instabilities, following their non‑linear development with analysis and numerical relativity, and identifying gravitational‑wave signatures that would uniquely signal this pathway.

To connect rigorous theory with data, we focus on the ringdown—the relaxation of a perturbed black hole to its stationary state, which, at late times can be described by quasinormal modes (the exponentially-damped sinusoidal tones of a perturbed black hole). We will clarify when this quasi-normal description is reliable by dissecting the spectral instability of the pseudospectrum, quantifying how tiny perturbations—arising from non‑linear general relativity, ordinary or dark matter, or beyond‑Einstein effects—can shift or destabilize modes, and modeling their observability. We will make precise the link between eikonal quasinormal modes and the photon ring/shell (the unstable orbit of light) by computing ringdown amplitudes for inspirals into Kerr and constructing an “eikonal ringdown waveform,” enabling detailed comparisons with extreme‑mass‑ratio signals. Beyond linear theory, we will study the excitation of non‑linear quasinormal modes and unexpectedly large early‑time tails, build waveform models that include these effects, and test them against observations.

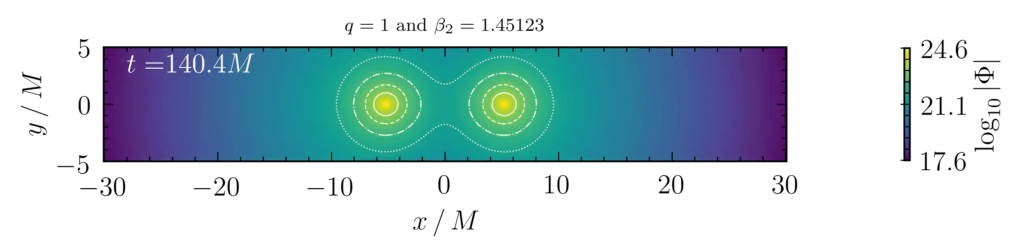
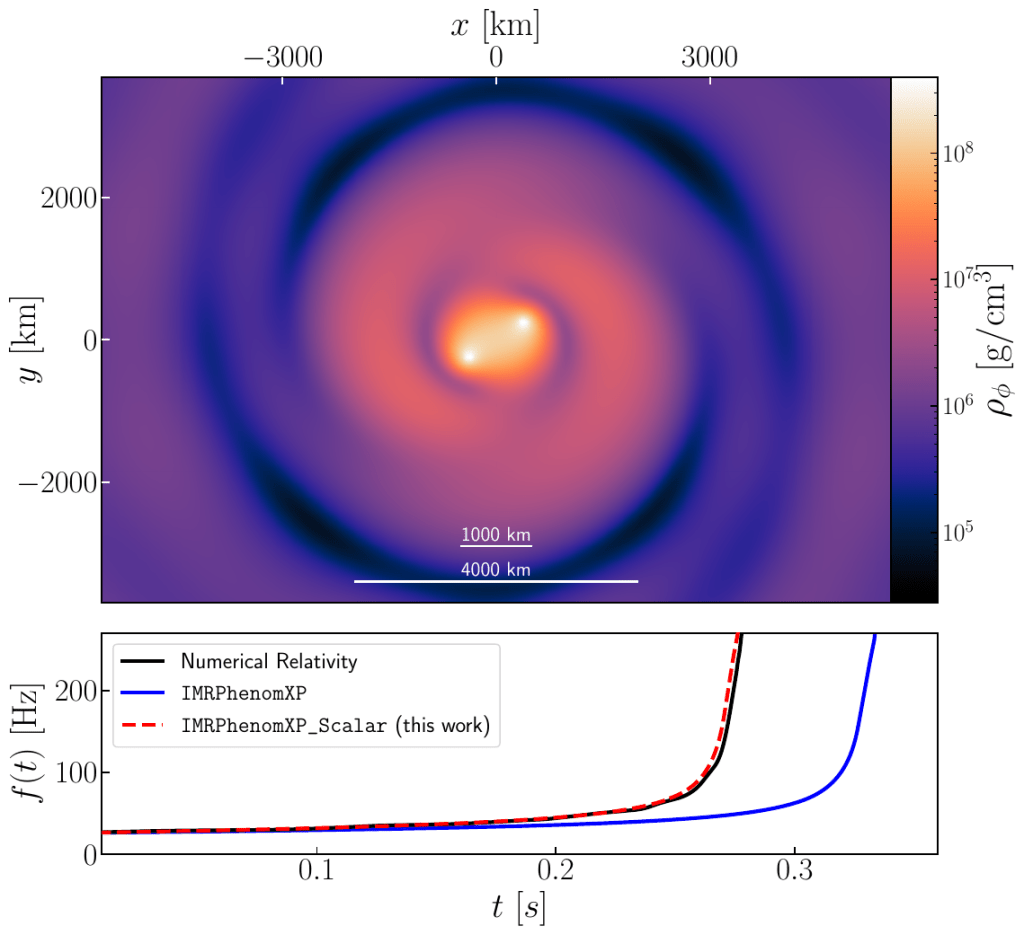
Strong Tests pushes gravity tests into the fully nonlinear regime of black‑hole coalescences, where deviations from general relativity (GR) would be most visible. Using new numerical methods to evolve modified‑gravity spacetimes—including higher‑derivative theories—we will simulate the late inspiral, merger, and ringdown of binary black holes and classify their gravitational‑wave signatures, especially phase shifts (“dephasing”) across the coalescence. These simulations also act as theory diagnostics, exposing pathologies such as instabilities that drive a theory outside its effective‑field‑theory (EFT) regime of validity so we can focus on consistent models. For viable theories, we will conduct black‑hole spectroscopy beyond Einstein: mapping the quasinormal‑mode spectrum and studying nonlinear content, tails, and memory in the ringdown, with benchmarks against semi‑analytical and perturbative calculations for rapidly rotating black holes. The resulting waveforms will power both targeted model comparisons and theory‑agnostic pipelines, and will underpin inspiral–merger–ringdown models that extend the parameterized post‑Einsteinian (ppE) framework for use on current and future gravitational‑wave data, with distinguishability from GR assessed via Bayesian inference and model selection.

To ensure robust conclusions, we will separate genuine beyond‑Einstein effects from astrophysical environments that can mimic them. Black‑hole binaries need not merge in vacuum: nearby third bodies, circumbinary accretion disks, ultralight scalar clouds grown through superradiance, or surrounding dark matter can all imprint the waveform—typically more strongly in the early inspiral than in the merger—providing a strategy to disentangle environmental signatures from nonlinear gravitational physics. In parallel, we will probe whether strong‑field gravity itself can invalidate standard EFT assumptions near (near‑)extremal horizons, where even tiny higher‑derivative couplings may amplify to produce very fields for infalling observers, leaving observable traces. Finally, leveraging recent mathematical and computational advances, we will simulate gravitational collapse outside GR to test whether violations of the usual positivity/energy conditions can avert singularity formation, or instead signal the limits of beyond‑Einstein corrections—thereby guiding extensions of the singularity theorems and delivering end‑to‑end strong‑field tests of gravity.

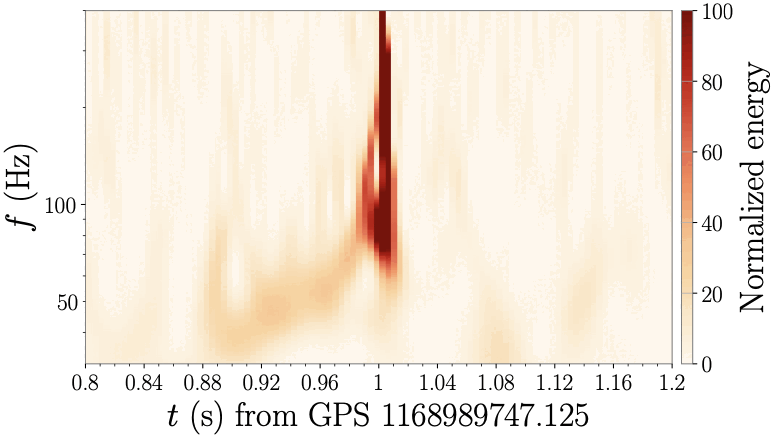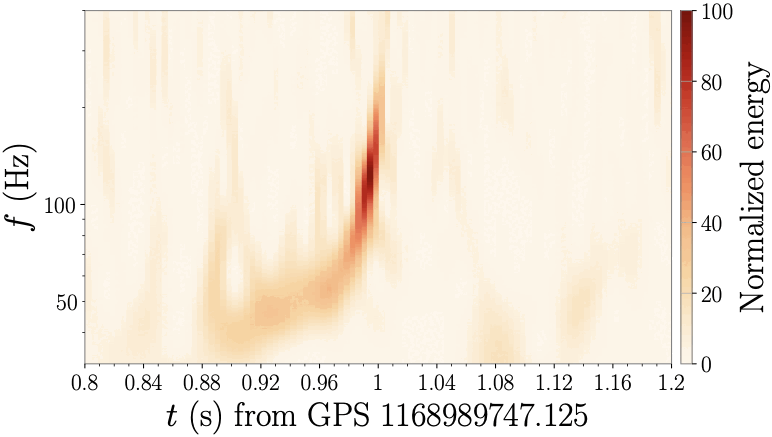
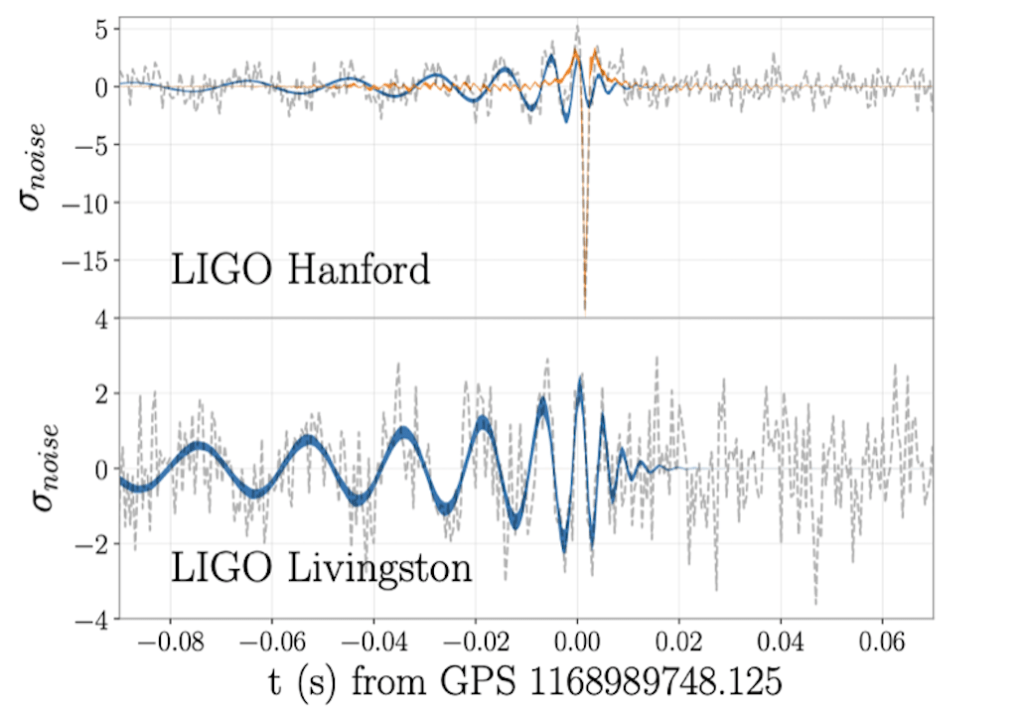
The Strong Observations working group will turn gravitational‑wave observations into robust tests of strong gravity while guarding against false positives from the instruments. We will quantify how data gaps, time‑varying and non‑Gaussian noise, and calibration errors could bias searches for beyond‑Einstein signatures in the late inspiral and in the non‑linear ringdown. Because binaries of different total masses and redshifts probe different frequencies, they sample detector noise differently; we will exploit this, and the expectation that true beyond‑GR effects should recur across black‑hole mergers and across detectors, to separate astrophysical anomalies from detector artifacts and to develop mitigation strategies. In parallel, we will pursue agnostic, effective‑field‑theory–motivated tests by extending the parameterized‑post‑Einsteinian (ppE) framework, which organizes deviations by the order at which they first modify the waveform and by how they scale with the system’s total mass. If the data favor a deviation with a specific power‑law exponent, we can rule out broad classes of theories and strengthen discrimination against systematics. These tests will be deployed on single events and—through hierarchical population analyses that account for mass ratio and spin—across the growing event catalog, mapping which classes of anomalies are easiest to detect in current and future detectors.

To remain sensitive to surprises, we will also conduct unmodeled searches for novel strong‑gravity phenomena. We will combine trans‑dimensional Bayesian inference—reversible‑jump Markov chain Monte Carlo that flexibly adjusts model complexity—with modern machine‑learning tools that learn fast, flexible posterior approximations from simulations (normalizing‑flow networks). This machine‑learning‑enhanced framework will let us traverse both model and parameter spaces, distinguish new physics from unmodeled instrumental behavior, and search for non‑linearities in mergers and ringdown. We will apply it to current data to obtain the tightest constraints—or first detections, if present—of physics beyond general relativity. Finally, by injecting numerically simulated beyond‑Einstein waveforms and recovering them with our unmodeled pipeline, we will build a “dictionary” that maps any recovered anomalies to concrete physical effects, allowing us to translate detections or upper limits into statements about underlying symmetries and operators in candidate theories.